Glencoe geometry chapter 8 answer key – Delving into the realm of Glencoe Geometry Chapter 8, we embark on a captivating journey to unravel the enigmatic world of similarity. This chapter holds the key to understanding the intricate relationships between triangles, revealing their hidden patterns and unlocking a treasure trove of real-world applications.
Join us as we delve into the depths of similarity, exploring its profound implications in geometry and beyond.
Chapter 8 embarks on an exploration of the fundamental concept of similarity in triangles, laying the groundwork for a comprehensive understanding of its significance. We delve into the intricacies of similarity theorems, empowering you to confidently apply them in diverse scenarios.
Moreover, we unravel the art of proving triangle similarity, equipping you with the tools to navigate this geometrical landscape with precision.
Key Concepts in Chapter 8: Glencoe Geometry Chapter 8 Answer Key
Chapter 8 of Glencoe Geometry delves into the fundamental concept of similarity in triangles. Similarity, a geometric relationship between figures, implies that the shapes are identical in form but not necessarily in size. This chapter explores the various theorems and methods used to establish triangle similarity, along with their applications in real-world scenarios.
Triangle Similarity Theorems
Triangle similarity theorems provide criteria for determining whether two triangles are similar. These theorems include:
- Side-Side-Side (SSS) Similarity Theorem:If the corresponding sides of two triangles are proportional, the triangles are similar.
- Side-Angle-Side (SAS) Similarity Theorem:If two pairs of corresponding sides and the included angle of two triangles are congruent, the triangles are similar.
- Angle-Angle-Angle (AAA) Similarity Theorem:If the corresponding angles of two triangles are congruent, the triangles are similar.
Methods for Proving Triangle Similarity
In addition to the similarity theorems, various methods can be used to prove triangle similarity. These methods include:
- Using Similarity Transformations:Applying transformations such as dilation, rotation, or translation can create similar triangles from a given triangle.
- Using Proportions:Establishing proportions between corresponding sides or angles can lead to the application of similarity theorems.
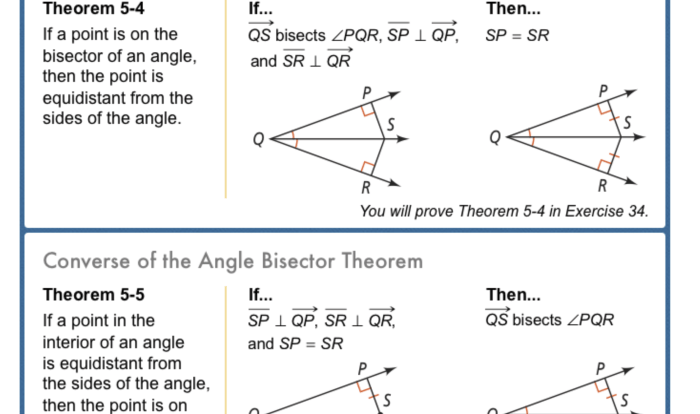
- Using Angle Bisectors and Perpendicular Bisectors:Bisecting angles or perpendicularly bisecting sides can create congruent triangles, which can then be used to prove similarity.
Applications of Triangle Similarity
Triangle similarity finds practical applications in various fields, such as:
- Architecture:Scaling architectural plans and designs while maintaining the proportions of the original.
- Engineering:Designing and constructing structures that are geometrically similar to withstand specific loads and forces.
- Art and Design:Creating visually appealing and harmonious compositions by utilizing similar shapes and proportions.
Applications of Similarity
Similarity has wide applications in solving real-world problems, from engineering to art. It allows us to use the properties of similar figures to find missing measurements and make predictions.
Finding Missing Measurements
If two figures are similar, their corresponding sides are proportional. This means that we can use the ratio of the corresponding sides to find missing measurements. For example, if we know the height and width of a rectangle and the height of a similar rectangle, we can use the ratio of the heights to find the width of the similar rectangle.
Scale Factor
The scale factor between two similar figures is the ratio of the corresponding sides. It tells us how much larger or smaller one figure is compared to the other. The scale factor is important because it allows us to make predictions about the measurements of one figure based on the measurements of another.
Solving Equations with Similarity

When working with similar triangles, solving equations involving their side lengths is crucial. Similarity allows us to establish proportions between corresponding sides, enabling us to determine unknown side lengths or angles.
Establishing Proportions
To solve equations using similarity, we first establish proportions between corresponding sides. For example, if we have two similar triangles with side lengths a, b, and cfor one triangle, and x, y, and zfor the other, then the following proportions hold true:
- a/x = b/y = c/z
These proportions allow us to solve for unknown side lengths.
Solving for Unknown Side Lengths
To solve for an unknown side length, we use the established proportions. For example, if we know the values of a, b, and y, and we want to find the value of x, we can use the proportion a/x = b/y:
- a/x = b/y
- Cross-multiply: ax = by
- Solve for x: x = (by)/a
This process can be applied to any unknown side length.
Example
Consider two similar triangles with side lengths a= 5 cm, b= 7 cm, c= 9 cm, and x= 10 cm. Find the value of y.
- a/x = b/y
- 5/10 = 7/y
- Cross-multiply: 5y = 70
- Solve for y: y = 14 cm
4. Advanced Similarity Concepts
In this section, we will delve deeper into the concept of similarity and explore its advanced applications.
Dilation and Similarity
Dilation is a transformation that changes the size of a figure but not its shape. A dilation is determined by a scale factor, which is the ratio of the length of the dilated figure to the length of the original figure.
When a figure is dilated by a scale factor of k, the resulting figure is similar to the original figure.
Properties of Similar Polygons
Similar polygons have the following properties:
- Corresponding sides are proportional.
- Corresponding angles are congruent.
- The ratio of the areas of similar polygons is equal to the square of the scale factor.
Applications of Similarity in Geometric Constructions
Similarity has numerous applications in geometric constructions, including:
- Enlarging or reducing figures
- Constructing similar figures
- Dividing a line segment into a given ratio
5. Practice and Review

This section provides a comprehensive review of the key concepts and theorems covered in Chapter 8, Applications of Similarity.
Key Concepts and Theorems, Glencoe geometry chapter 8 answer key
The following table summarizes the key concepts and theorems in Chapter 8:
| Concept | Theorem |
|---|---|
| Similar Figures | If two figures are similar, then their corresponding angles are congruent and their corresponding sides are proportional. |
| Scale Factor | The scale factor between two similar figures is the ratio of the lengths of their corresponding sides. |
| Area and Volume of Similar Figures | The ratio of the areas of two similar figures is the square of the scale factor. The ratio of the volumes of two similar figures is the cube of the scale factor. |
| Midsegment Theorem | The midsegment of a triangle is parallel to the third side and half its length. |
| Angle Bisector Theorem | The angle bisector of a triangle divides the opposite side into segments that are proportional to the adjacent sides. |
Practice Problems
Solve the following practice problems:
- Two triangles are similar. The first triangle has sides of length 3, 4, and 5. The second triangle has sides of length 6, 8, and 10. Find the scale factor between the two triangles.
- A rectangular prism has a length of 10 cm, a width of 5 cm, and a height of 3 cm. A similar rectangular prism has a length of 15 cm. Find the volume of the second rectangular prism.
- Find the length of the midsegment of a triangle with sides of length 12 cm, 15 cm, and 18 cm.
- Find the ratio of the lengths of the segments created by the angle bisector of a triangle with sides of length 8 cm, 10 cm, and 12 cm.
Interactive Exercises
Complete the following interactive exercises to reinforce your understanding of similarity:
- Use the interactive applet to explore the relationship between the scale factor and the corresponding sides and angles of similar triangles.
- Use the interactive applet to explore the relationship between the scale factor and the areas and volumes of similar figures.
- Use the interactive applet to explore the properties of the midsegment and angle bisector of a triangle.
Q&A
What is the significance of similarity in geometry?
Similarity plays a pivotal role in geometry, as it establishes relationships between figures that maintain proportional dimensions. This enables us to solve problems involving missing measurements, scale factors, and geometric constructions with greater accuracy and efficiency.
How can I prove that two triangles are similar?
There are several methods to prove the similarity of triangles, including the Side-Side-Side (SSS) Similarity Theorem, the Side-Angle-Side (SAS) Similarity Theorem, and the Angle-Angle-Angle (AAA) Similarity Theorem. Each theorem provides specific criteria that, when satisfied, establish the similarity of the triangles.
What are the applications of similarity in real-world scenarios?
Similarity finds practical applications in various fields, including architecture, engineering, and design. It enables architects to scale up or down building plans while maintaining the proportions, allows engineers to design structures that withstand forces, and empowers designers to create aesthetically pleasing objects with harmonious dimensions.